File talk:Venn Diagrams.PNG
Rims
I agree that it is good to make it clear what the role of the rims is in these visualizations, but I don't think rectangular cuts are the way to go. --Daniel Mietchen 02:39, 10 July 2011 (UTC)
- If you are talking about the rectangular "universal" set then I agree: It is irrelevant and should therefore be omitted.
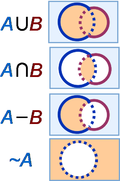
- If the boundaries are used to identify the "red" and the "blue" set then the complete coloured circles have to be present in all diagrams.
- For my taste the boundaries are much too thick -- they should be only thick enough to clearly show their colours.
- In the formulas, the symbols for the binary operations are too big. Compare
- Instead of one picture with 3 diagrams, three separate pictures would be more useful. Perhaps with circles of different sizes (and the forumla above or below the diagrams. In addition,
- a diagram for and (perhaps) also for the relative complement
- in the same graphical design would be useful.
- --Peter Schmitt 14:56, 10 July 2011 (UTC)
- See also the image Venn diagrams XY.PNG, in Venn diagram, which has the same format. There are undoubtedly many ways to approach the picture, and I'd guess the way to decide what to do is to compare different actual pictures. There are a few things to notice:
- The pictures in the articles are reduced in size, and the tiny details of the regions where the rims intersect are not really an issue.
- The pictures are accurate. The sets are the interiors of the circles, and the rims constitute different but not entirely disjoint sets. In the intersection, for example, the points in the interior of one circle include some, but not all, of the points in the rim of the other circle. In the union, the points in the rims that also lie interior to one or the other circle are part of the sets of the interiors.
- Making the rims thinner has the effect of requiring a different method to distinguish between the sets, because the coloring of the rims becomes impossible to see at a reasonable figure size. If the sets are shaded differently or cross-hatched, or whatever, it seems to work well for the intersection because large regions of the two sets are not part of the intersection, but it doesn't work so well for the union because the entire two sets are taken by the union leaving no identifying markings for the individual sets.
- The universal set is mentioned in the articles, so it isn't exactly irrelevant. The source here suggests such an approach. See also Figure 1-7 here, Illustration 16 here, diagram 4 here, Figures 2.22 & 2.23 here, the discussion surrounding Figure 5.1 here and on and on. It appears that the choice of a rectangle for the universal set in Venn diagrams is very usual. John R. Brews 22:18, 10 July 2011 (UTC)
- See also the image Venn diagrams XY.PNG, in Venn diagram, which has the same format. There are undoubtedly many ways to approach the picture, and I'd guess the way to decide what to do is to compare different actual pictures. There are a few things to notice:
- The thickness of the boundary is a matter of taste (but it looks thick to me even in its reduced size). The only purpose of the boundary line is to separate the interior from the exterior -- therefore it should be as thin as possible. (Incicdently, it is thin in all the examples you cite ...)
- But this is not a critical flaw. The critical flaw is that the diagrams for union and set difference do not show the full coloured circles (as it is correctly done for the intersection).
- Showing a universal set is fine if a universal set is needed. But usually a universe is avoided and not used in mathematics. (For instance, your favourite ZF set theory does not have a universe.) Therefore it should not be used when the primitive set operations are illustrated.
- --Peter Schmitt 22:54, 10 July 2011 (UTC)
- On the colours: It may be my screen but, for me, the colours are not as different as they could be. In particular, at first glance I did not even notice that the letters are coloured, too. Perhaps lighter colours would look more different? (Instead of pink a light grey could be used -- but this is my personal taste, again.) --Peter Schmitt 23:04, 10 July 2011 (UTC)
← ←Unindent Hi Peter: I suspect that you are discussing an earlier version of the image. The intersection no longer shows the full circles. The reason is that I decided to redefine the sets A and B as the interiors of the circles, rather than the interiors and their containing rims. Thus there are actually not only the sets A and B and the universal set, but also the sets RimA and RimB. The set A then can contain points in set RimB if RimB has a position causing it to enter the circle defining set A.
I don't think having four sets instead of two is desirable, but the first approach with set A and set RimA combined seemed to cause some troubles with the diagrams - maybe I should think some more about that; my guess is that most readers won't ever notice the Rim sets, though. John R. Brews 23:12, 10 July 2011 (UTC)
I see that the diagram wasn't updated properly; I have now fixed that. John R. Brews 23:56, 10 July 2011 (UTC)
- John, it is completely misleading and confusing to consider the "rim" as separate sets (strips with non-zero breadth). If you do so, both the diagrams for the union and the difference are definitely false. You need to draw a boundary in order to indicate the regions that they enclose. Ideally, they are 1-dimensinal curves that only habe length but no breadth. Then it is irrelevant for the interpretation of the diagrams if you consider the regions as closed (with their boundary) or open (without their boundary). But you seem to miss my main point: In all three diagrams the complete "rims" or boundaries have to be drawn in their colour. In the diagrams for the union and for the difference the blue circle is not complete and the red circle changes colour! --Peter Schmitt 00:20, 11 July 2011 (UTC)
- Perhaps I need some help here. This is my scenario:
- Set RimB is all points in the rim of the red circle and are, of course, red. Set A is all points interior to the blue circle, and are white.
- Let's look at the Intersection. When the red RimB crosses the blue boundary and enters the white realm interior to the blue circle, those points inside the blue circle become points of not only set RimB but also points of set A. Their color is then ambiguous: it could equally be be red or white. These points of RimB interior to the blue circle also are part of set A, which is white. Of course, these dual citizenship points could be taken as either color, but if one is trying to depict the intersection of set A with set B, it seemed to me that all the set A points must be emphasized, so white is chosen.
- Maybe you have a different way to look at the matter? One could continue to show the points of set RimB as red. It would not change the orange-colored intersection.
- However, to obtain the correct Union A∪B, the points of set RimB interior to the blue circle are now part of set A and hence of the union A∪B, and must become orange.
- Likewise, in the Difference, the points of set RimB interior to the blue circle must become orange because they now are points of set A and hence part of the difference A−B.
- Do you have a different view? John R. Brews 03:25, 11 July 2011 (UTC)
- I have added a footnote to Venn diagram about this annoyance, and referred to it in Set (mathematics). John R. Brews 16:25, 11 July 2011 (UTC)
- I have modified the picture to make it more accommodating to either the view that the rims have points or that they do not have their own points. Is it better? John R. Brews 18:10, 11 July 2011 (UTC)
- This is definitely better, but the "rims" should be fully drawn, instead of dotted in the interior.
- I don't see a need for versions with different set names. As I said, separate pictures for each operation would be useful. And perhaps also versions without formula.
- Some stylistic comments still apply, I think.
- And don't bother with the "rims"! They are only a means to indicate the regions occupied by the sets. What do you need in the diagram? You have to indicate two sets. You do this by drawing their boundary (using two colours to better identify them). And you have to indicate the result of the operations. You do this by colouring the region. You do not need a universal set. Avoid all complications. --Peter Schmitt 00:20, 12 July 2011 (UTC)
- Peter: You describe the situation pointed out in the text of Set (mathematics) and Venn diagram where the perimeters simply separate points but have no points of their own. That is all that is necessary, as you point out. However, it is a natural question to wonder what happens if the boundaries actually contain points, as any geometric figure is always made of points, and real boundaries in any real figure contain points. The figures presented allow that question to be answered using dashed lines for segments of the rim that have dual citizenship, and the answer is provided.
- You object that the universal set is unnecessary, but above I have provided six or so of dozens of texts that do include the universal set in the manner shown, indicating these authors' judgment that this depiction is helpful. And the CZ articles also refer to the universal set, so its inclusion in the figure fits the text.
- I believe we are simply of a different mind regarding matters of taste here. John R. Brews 03:10, 12 July 2011 (UTC)
← ← <noindent> Peter: I have rewritten the article on Venn diagrams following your suggestions. It fits better with the discussion of more complicated diagrams. It uses the figure at right. John R. Brews 15:08, 12 July 2011 (UTC)