Quantum computation

Throughout this article The Many Worlds Interpretation(MWI) of quantum mechanics is used.

Differences with classical computation

In classical computation there is the concept of a discrete bit, taking only one of two values. However , the world which classical physics describes is that of continua. Thus this is obviously not an ideal way of attempting to describe or simulate the world in which we live. Feynman was the first to consider the idea of a quantum computer being necessary to simulate the quantum mechanical world in which we live.

Quantum computers & information theory

The quantum mechanical analogue of the classical bit is the qubit. A qubit is an actual physical system, all of whose observables are Boolean.

Quantum Algorithms

An algorithm is a hardware-independant recipe for performing a particular computation. A program is a way of preparing a specific computer to do such a task. Algorithms for quantum computers offer a wider range of computational tasks which may be solved by the use of interference. Some of the new possibilities which are opened up may prove to have drastic consequences for the future: e.g. Shor's algorithm relevance to cryptography.

Oracles

An oracle is a black box which it is impossible to look inside and performs a particular function f on the input qubits in a time which is independant of the particular input. It is not possible. They are used to simplify the analysis of algorithms as the specific nature of how a task is performed is irrelevant due to the criterion of hardware-independance. The oracle must of course be reversible as the laws of QM do not make a distinction between forwards and backwards time (i.e. time does not have 'an arrow').

Dynamics of quantum gates in Schrödinger picture

NB In the Schrödinger picture the state vector evolves in the following manner:
$\left|\psi (t+1)\right\rangle =U\left|\psi (t)\right\rangle$
where $U$ is the characteristic unitary matrix of the gate.

NOT

$\left|a\right\rangle \to \left|-a\right\rangle ,\qquad a=\pm 1$
So if $\left|a\right\rangle =\left|\psi (0)\right\rangle$ then $\left|-a\right\rangle =\left|\psi (1)\right\rangle$

Controlled Not, CNOT

This i a two input gate where whether the NOT operation is performed on the second is dependant (i.e. controlled) by the value of the first input bit which is unchanged.
$\left|x\right\rangle \left|y\right\rangle \equiv \left|x,y\right\rangle \to \left|x,xy\right\rangle$

Hadamard gate, H

The Hadamard gate, normally denoted as H, creates an equally weighted superposition of the $\left|1\right\rangle$ and $\left|-1\right\rangle$ states. There is no classical analogue of it.

$\left|1\right\rangle \to {\frac {1}{\sqrt {2}}}(\left|1\right\rangle +\left|-1\right\rangle )$
$\left|-1\right\rangle \to {\frac {1}{\sqrt {2}}}(\left|1\right\rangle -\left|-1\right\rangle )$
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^2=I} i.e the Hadamard gate is self-inverse.

Oracle

An oracle which performs the function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} has the following dynamics in the Schrödinger picture. The value of y is normally set to one so that the output is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | x,y \right \rangle \to \left | x, yf(x) \right \rangle}

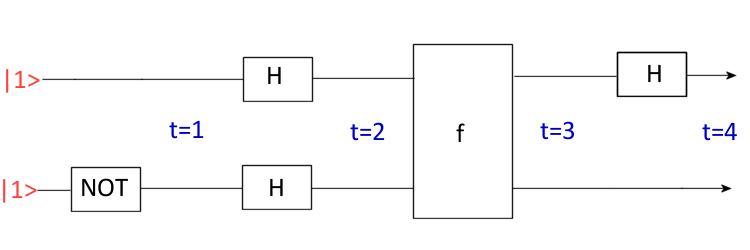
Deutsch algorithm

Let us create an oracle which performs the following function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f: \{-1,1\} \mapsto \{-1,1\}}
There are four possiblities for this function:

1. identity: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \mapsto x}
2. not: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \mapsto -x}
3. output -1: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \mapsto -1}
4. output 1: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \mapsto 1}

Computational task: To determine if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)=f(-1)} .
This is equivalant to trying to determine Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)f(-1)} without looking inside the oracle above. Classically this may be done by consulting the oracle twice. [diagram of classical situation] However, using quantum computation the oracle need only be consulted once.

(N.B. For the analysis of algorithms, the Schrödinger picture is often preferable and thus shall be used here. It is of course still possible to use the Heisenberg picture.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | \psi(0) \right \rangle = \left | 1,1 \right \rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | \psi(1) \right \rangle = \left | 1,-1\right \rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | \psi(2) \right \rangle = \frac{1}{2}(\left | 1 \right \rangle + \left | -1 \right \rangle)(\left | 1 \right \rangle - \left | -1 \right \rangle) = \frac{1}{2}(\left | 1,1 \right \rangle + \left | -1,1 \right \rangle - \left | 1,-1 \right \rangle - \left | -1,-1 \right \rangle) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | \psi(3) \right \rangle = \frac{1}{2}(\left | 1,f(1) \right \rangle + \left | -1,f(1) \right \rangle - \left | 1,-f(-1) \right \rangle - \left | -1,-f(-1) \right \rangle)}

Now we must examine the two possiblities 1) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)=f(-1)} and 2) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)=-f(-1)}
1. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)=f(-1)=f}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \left | \psi(3) \right \rangle = \frac{1}{2}(\left | 1,f \right \rangle + \left | -1,f \right \rangle - \left | 1,-f \right \rangle - \left | -1,-f \right \rangle) = \frac{1}{2}(\left | 1 \right \rangle + \left | -1 \right \rangle)(\left | f \right \rangle - \left | -f \right \rangle)}
2. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)=-f(-1)=f}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \left | \psi(3) \right \rangle = \frac{1}{2}(\left | 1 \right \rangle - \left | -1 \right \rangle)(\left | f \right \rangle - \left | -f \right \rangle)}

In each of these cases the state vector when t=3 is a superposition of two pure states: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{2}}(\left | 1 \right \rangle \pm \left | -1 \right \rangle)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{2}}(\left | f \right \rangle \pm \left | -f \right \rangle)} . The purpose of the final Hadamard gate is to differentiate between the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{2}}(\left | 1 \right \rangle \pm \left | -1 \right \rangle)} and thus determine whether Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)=f(-1)} or not.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\frac{1}{\sqrt{2}}(\left | 1 \right \rangle + \left | -1 \right \rangle)= \left | 1 \right \rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\frac{1}{\sqrt{2}}(\left | 1 \right \rangle - \left | -1 \right \rangle)= \left | -1 \right \rangle}

Thus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | \psi(4) \right \rangle = \frac{1}{\sqrt{2}}\left | f(1)f(-1) \right \rangle(\left | f \right \rangle - \left | -f \right \rangle}

References

Based on a talk given by Charles Blackham to 6P at Winchester College, UK on 7/3/07

1. Lectures on Quantum Computation by David Deutsch
2. Cambridge Centre for Quantum Computation