User:John R. Brews/Coriolis force: Difference between revisions
imported>John R. Brews |
imported>John R. Brews No edit summary |
||
| Line 10: | Line 10: | ||
When considering atmospheric or oceanic dynamics, the vertical velocity is small and the vertical component of the Coriolis acceleration is small compared to gravity. For such cases, only the horizontal (East and North) components matter. The restriction of the above to the horizontal plane is (setting ''v<sub>u</sub>''=0): | When considering atmospheric or oceanic dynamics, the vertical velocity is small and the vertical component of the Coriolis acceleration is small compared to gravity. For such cases, only the horizontal (East and North) components matter. The restriction of the above to the horizontal plane is (setting ''v<sub>u</sub>''=0): | ||
:<math> \boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n\end{pmatrix}\ ,</math> <math>\boldsymbol{ | :<math> \boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n\end{pmatrix}\ ,</math> <math>\boldsymbol{ a_{Cor}} = \begin{pmatrix} v_n \\ -v_e\end{pmatrix}\ f\ , </math> | ||
where ''f'' = {{nowrap|2''ω'' sin''φ''}} is called the ''Coriolis parameter''.<ref name=Norbury> | where ''f'' = {{nowrap|2''ω'' sin''φ''}} is called the ''Coriolis parameter''.<ref name=Norbury> | ||
| Line 29: | Line 29: | ||
As a different case, consider equatorial motion setting φ = 0°. In this case, '''Ω''' is parallel to the North or ''n''-axis, and: | As a different case, consider equatorial motion setting φ = 0°. In this case, '''Ω''' is parallel to the North or ''n''-axis, and: | ||
:<math>\boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\ ,</math> <math>\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ ,</math> <math>\boldsymbol{ | :<math>\boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\ ,</math> <math>\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ ,</math> <math>\boldsymbol{ a_{Cor}} =-2\boldsymbol{\Omega \times v}= 2\,\omega\, \begin{pmatrix}-v_u \\0 \\ v_e \end{pmatrix}\ .</math> | ||
Accordingly, an eastward motion (that is, in the same direction as the rotation of the sphere) provides an upward acceleration known as the [[Eötvös effect]],<ref name=Talwani> | Accordingly, an eastward motion (that is, in the same direction as the rotation of the sphere) provides an upward acceleration known as the [[Eötvös effect]],<ref name=Talwani> | ||
Revision as of 13:03, 5 March 2011
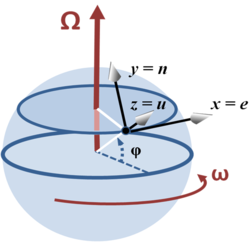
Rotating sphere
Consider a location with latitude φ on a sphere that is rotating around the north-south axis.[1] A local coordinate system is set up with the x-axis horizontally due east, the y-axis horizontally due north and the z-axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system (listing components in the order East (e), North (n) and Upward (u)) are:
When considering atmospheric or oceanic dynamics, the vertical velocity is small and the vertical component of the Coriolis acceleration is small compared to gravity. For such cases, only the horizontal (East and North) components matter. The restriction of the above to the horizontal plane is (setting vu=0):
where f = 2ω sinφ is called the Coriolis parameter.[2]
By setting vn = 0, it can be seen immediately that (for positive φ and ω) a movement due east results in an acceleration due south. Similarly, setting ve = 0, it is seen that a movement due north results in an acceleration due east. In general, observed horizontally, looking along the direction of the movement causing the acceleration, the acceleration always is turned 90° to the right and of the same size regardless of the horizontal orientation. That is:[3][4]
| ‘ | On a merry-go-round in the night Coriolis was shaken with fright |
’ |
—David Morin, Eric Zaslow, E'beth Haley, John Golden, and Nathan Salwen | ||
As a different case, consider equatorial motion setting φ = 0°. In this case, Ω is parallel to the North or n-axis, and:
Accordingly, an eastward motion (that is, in the same direction as the rotation of the sphere) provides an upward acceleration known as the Eötvös effect,[5] and an upward motion produces an acceleration due west.
Notes
- ↑ William Menke & Dallas Abbott (1990). Geophysical Theory. Columbia University Press, 124–126. ISBN 0231067925.
- ↑ For a discussion of the role of the Coriolis parameter in ocean dynamics see John Norbury (2002). “§6.3 Further geometric and Coriolis approximations”, Large-scale Atmosphere-ocean Dynamics: Analytical methods and numerical models. Cambridge University Press, p. 35 ff. ISBN 052180681X.
- ↑ David Morin, Eric Zaslow, Elizabeth Haley, John Goldne, and Natan Salwen (2 December 2005). Limerick – May the Force Be With You. Weekly Newsletter Volume 22, No 47. Department of Physics and Astronomy, University of Canterbury. Retrieved on 2009-01-01.
- ↑ David Morin (2008). Introduction to classical mechanics: with problems and solutions. Cambridge University Press. ISBN 0521876222.
- ↑ The Eötvös effect must be corrected for in determining the effects of gravity aboard ship. See Manik Talwani (1906). “Gravity measurements aboard surface ships: Eötvös effect”, Hyman Orlin, ed.: Gravity anomalies: unsurveyed areas. American Geophysical Union, p. 46.
Contributed by myself in June 2008, for example, here here, added Limerick