User talk:Paul Wormer/scratchbook1: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
'''Entropy''' is a function of the state of a [[thermodynamics|thermodynamic system]]. It is a size-extensive<ref>A size-extensive property of a system becomes ''x'' times larger when the system is enlarged by a factor ''x'', provided all intensive parameters remain the same upon the enlargement. Intensive parameters, like temperature and pressure, are independent of size.</ref> quantity with dimension energy divided by temperature ([[SI]] unit: [[joule]]/K). Entropy has no clear analogous mechanical meaning—unlike volume, a similar size-extensive state parameter with dimension energy divided by pressure. Moreover entropy cannot directly be measured, there is no such thing as an entropy meter, whereas state parameters as volume and temperature are easily determined. Consequently entropy is one of the least understood concepts in physics.<ref>It is reported that in a conversation with Claude Shannon, John von Neumann | '''Entropy''' is a function of the state of a [[thermodynamics|thermodynamic system]]. It is a size-extensive<ref>A size-extensive property of a system becomes ''x'' times larger when the system is enlarged by a factor ''x'', provided all intensive parameters remain the same upon the enlargement. Intensive parameters, like temperature, density, and pressure, are independent of size.</ref> quantity with dimension [[energy]] divided by temperature ([[SI]] unit: [[joule]]/K). Entropy has no clear analogous mechanical meaning—unlike volume, a similar size-extensive state parameter with dimension energy divided by pressure. Moreover entropy cannot directly be measured, there is no such thing as an entropy meter, whereas state parameters as volume and temperature are easily determined. Consequently entropy is one of the least understood concepts in physics.<ref>It is reported that in a conversation with Claude Shannon, John (Johann) von Neumann said: "In the second place, and more important, nobody knows what entropy really is [..]”. M. Tribus, E. C. McIrvine, ''Energy and information'', Scientific American, vol. '''224''' (September 1971), pp. 178–184.</ref> | ||
{{Image|Carnot title page.jpg|right|300px}} | {{Image|Carnot title page.jpg|right|300px}} | ||
The state variable "entropy" was introduced by [[Rudolf Clausius]] in | The state variable "entropy" was introduced by [[Rudolf Clausius]] in the 1860s<ref>R. J. E. Clausius, ''Abhandlungen über die mechanische Wärmetheorie'' [Treatise on the mechanical theory of heat], two volumes, F. Vieweg, Braunschweig, (1864-1867).</ref> | ||
when he gave a mathematical formulation of the [[second law of thermodynamics]]. He derived the name from the classical Greek ἐν + τροπή (en = in, at; tropè = change, transformation). On purpose Clausius chose a term similar to "energy", because of the close relationship between the two concepts. | |||
The traditional way of introducing entropy is by means of a Carnot engine, an abstract engine conceived by [[Sadi Carnot]] | The traditional way of introducing entropy is by means of a Carnot engine, an abstract engine conceived in 1824 by [[Sadi Carnot]]<ref>S. Carnot, ''Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (Reflections on the motive power of fire and on machines suited to develop that power)'', Chez Bachelier, Paris (1824).</ref> as an idealization of a steam engine. Carnot's work foreshadowed the [[second law of thermodynamics]]. The "engineering" manner of introducing entropy through an engine will be discussed below. In this approach, entropy is the amount of [[heat]] (per degree kelvin) gained or lost by a thermodynamic system that makes a transition from one state to another. | ||
In | In 1877 [[Ludwig Boltzmann]]<ref> L. Boltzmann, ''Über die Beziehung zwischen dem zweiten Hauptsatz der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht'', [On the relation between the second fundamental law of the mechanical theory of heat and the probability calculus with respect to the theorems of heat equilibrium] Wiener Berichte vol. '''76''', pp. 373-435 (1877)</ref> gave a definition of entropy in the context of the kinetic gas theory, a branch of physics that developed into statistical thermodynamics. Boltzmann's definition of entropy was furthered by [[John von Neumann]]<ref>J. von Neumann, ''Mathematische Grundlagen der Quantenmechnik'', [Mathematical foundation of quantum mechanics] Springer, Berlin (1932)</ref> to a quantum statistical definition. The quantum statistical point of view, too, will be reviewed in the present article. In the statistical approach the entropy of an isolated (constant energy) system is ''k''<sub>B</sub> ln''Ω'', where ''k''<sub>B</sub> is [[Boltzmann's constant]], ''Ω'' is the number of different wave functions of the system belonging to the system's energy (''Ω'' is the degree of degeneracy, the probability that a state is described by one of the ''Ω'' wave functions), and the function ln stands for the natural (base ''e'') [[logarithm]]. | ||
Not satisfied with the engineering type of argument, the mathematician [[Constantin Carathéodory]] gave in 1909 a new axiomatic formulation of entropy and the second law.<ref>C. Carathéodory, ''Untersuchungen über die Grundlagen der Thermodynamik'' [Investigation on the foundations of thermodynamics], Mathematische Annalen, vol. '''67''', pp. 355-386 (1909).</ref> | Not satisfied with the engineering type of argument, the mathematician [[Constantin Carathéodory]] gave in 1909 a new axiomatic formulation of entropy and the second law.<ref>C. Carathéodory, ''Untersuchungen über die Grundlagen der Thermodynamik'' [Investigation on the foundations of thermodynamics], Mathematische Annalen, vol. '''67''', pp. 355-386 (1909).</ref> His theory was based on [[Pfaffian differential equations]]. His axiom replaced the earlier Kelvin-Planck and the equivalent Clausius formulation of the second law and did not need Carnot engines. Caratheodory's work was taken up by [[Max Born]],<ref>M. Born, Physikalische Zeitschrift, vol. 22, p. 218, 249, 282 (1922)</ref> and it is treated in a few textbooks.<ref>H. B. Callen, ''Thermodynamics and an Introduction to Thermostatistics.'' John Wiley and Sons, New York, 2nd edition, (1965); E. A. Guggenheim, ''Thermodynamics'', North-Holland, Amsterdam, 5th edition (1967)</ref> Since it requires more mathematical knowledge than the traditional approach based on Carnot engines, and since this mathematical knowledge is not needed by most students of thermodynamics, the traditional approach is still dominant in the majority of introductory works on thermodynamics. | ||
== | ==Classical definition== | ||
The state (a point in state space) of a thermodynamic system is characterized by a number of variables, such as [[pressure]] ''p'', [[temperature]] ''T'', amount of substance ''n'', volume ''V'', etc. Any thermodynamic parameter can be seen as a function of an arbitrary independent set of other thermodynamic variables, hence the terms "property", "parameter", "variable" and "function" are used interchangeably. The number of ''independent'' thermodynamic variables of a system is equal to the number of energy contacts of the system with its surroundings. | |||
The state | |||
An example of a reversible (quasi-static) energy contact is offered by the prototype thermodynamical system, a gas-filled cylinder with piston. Such a cylinder can perform work on its surroundings, | An example of a reversible (quasi-static) energy contact is offered by the prototype thermodynamical system, a gas-filled cylinder with piston. Such a cylinder can perform work on its surroundings, | ||
| Line 17: | Line 17: | ||
DW = pdV, \quad dV > 0, | DW = pdV, \quad dV > 0, | ||
</math> | </math> | ||
where ''dV'' stands for a small increment of the volume ''V'' of the cylinder, ''p'' is the pressure inside the cylinder and ''DW'' stands for a small amount of work. Work by expansion is a form of energy contact between the cylinder and its surroundings. This process can be reverted, the volume of the cylinder can be decreased, the gas is compressed and the surroundings perform work ''DW'' = ''pdV'' | where ''dV'' stands for a small increment of the volume ''V'' of the cylinder, ''p'' is the pressure inside the cylinder and ''DW'' stands for a small amount of work. Work by expansion is a form of energy contact between the cylinder and its surroundings. This process can be reverted, the volume of the cylinder can be decreased, the gas is compressed and the surroundings perform work ''DW'' = ''pdV'' < 0 ''on'' the cylinder. | ||
The small amount of work is indicated by ''D'', and not by ''d'', because ''DW'' is not necessarily a differential of a function. However, when we divide ''DW'' by ''p'' the quantity ''DW''/''p'' becomes obviously equal to the differential ''dV'' of the differentiable state function ''V''. State functions depend only on the actual values of the thermodynamic parameters (they are local), and ''not'' on the path along which the state was reached (the history of the state). Mathematically this means that integration from point 1 to point 2 along path I in state space is equal to integration along a different path II, | The small amount of work is indicated by ''D'', and not by ''d'', because ''DW'' is not necessarily a differential of a function. However, when we divide ''DW'' by ''p'' the quantity ''DW''/''p'' becomes obviously equal to the differential ''dV'' of the differentiable state function ''V''. State functions depend only on the actual values of the thermodynamic parameters (they are local in state space), and ''not'' on the path along which the state was reached (the history of the state). Mathematically this means that integration from point 1 to point 2 along path I in state space is equal to integration along a different path II, | ||
:<math> | :<math> | ||
V_2 - V_1 = {\int\limits_1\limits^2}_{{\!\!}^{(I)}} dV | V_2 - V_1 = {\int\limits_1\limits^2}_{{\!\!}^{(I)}} dV | ||
| Line 26: | Line 26: | ||
{\int\limits_1\limits^2}_{{\!\!}^{(II)}} \frac{DW}{p} | {\int\limits_1\limits^2}_{{\!\!}^{(II)}} \frac{DW}{p} | ||
</math> | </math> | ||
The amount of work (divided by ''p'') performed along path I is equal to the amount of work (divided by ''p'') along path II. This condition is necessary and sufficient that ''DW''/''p'' is a | The amount of work (divided by ''p'') performed reversibly along path I is equal to the amount of work (divided by ''p'') along path II. This condition is necessary and sufficient that ''DW''/''p'' is the differential of a state function. So, although ''DW'' is not a differential, the quotient ''DW''/''p'' is one. | ||
Reversible absorption of a small amount of heat ''DQ'' is another energy contact of a system with its surroundings; ''DQ'' is again not a differential of a certain function. In a completely analogous manner to ''DW''/''p'', the following result can be shown for the heat ''DQ'' (divided by ''T'') absorbed by the system along two different paths (along both paths the absorption is reversible): | Reversible absorption of a small amount of heat ''DQ'' is another energy contact of a system with its surroundings; ''DQ'' is again not a differential of a certain function. In a completely analogous manner to ''DW''/''p'', the following result can be shown for the heat ''DQ'' (divided by ''T'') absorbed reversibly by the system along two different paths (along both paths the absorption is reversible): | ||
<div style="text-align: right;" > | <div style="text-align: right;" > | ||
| Line 42: | Line 42: | ||
dS \;\stackrel{\mathrm{def}}{=}\; \frac{DQ}{T} | dS \;\stackrel{\mathrm{def}}{=}\; \frac{DQ}{T} | ||
</math> | </math> | ||
is the differential of a state variable ''S'', the ''entropy'' of the system. In | is the differential of a state variable ''S'', the ''entropy'' of the system. In the next subsection equation (1) will be proved from the Clausius/Kelvin principle. Observe that this definition of entropy only fixes entropy differences: | ||
:<math> | :<math> | ||
S_2-S_1 \equiv \int_1^2 dS = \int_1^2 \frac{DQ}{T} | S_2-S_1 \equiv \int_1^2 dS = \int_1^2 \frac{DQ}{T} | ||
| Line 51: | Line 51: | ||
</math> | </math> | ||
(For convenience sake only a single work term was considered here, namely ''DW'' = ''pdV'', work done ''by'' the system). | (For convenience sake only a single work term was considered here, namely ''DW'' = ''pdV'', work done ''by'' the system). | ||
The internal energy is an extensive quantity | The internal energy is an extensive quantity. The temperature ''T'' is an intensive property, independent of the size of the system. It follows that the entropy ''S'' is an extensive property. In that sense the entropy resembles the volume of the system. We reiterate that volume is a state function with a well-defined mechanical meaning, whereas entropy is introduced by analogy and is not easily visualized. Indeed, as is shown in the next subsection, it requires a fairly elaborate reasoning to prove that ''S'' is a state function, i.e., that equation [[#(1)|(1)]] holds. | ||
===Proof that entropy is a state function=== | ===Proof that entropy is a state function=== | ||
Equation [[#(1)|(1)]] gives the sufficient condition that the entropy ''S'' is a state function. The standard proof, as given now, is physical, by means of [[Carnot cycle]]s, and is based on the Clausius/Kelvin formulation of the second law given in the introduction. | |||
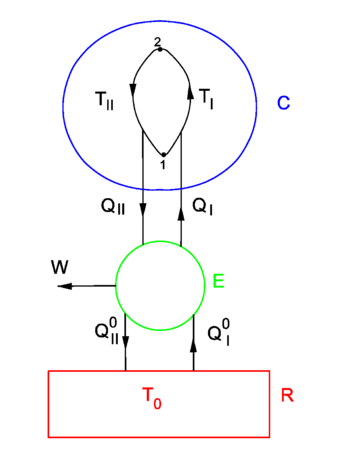
{{Image|Entropy.png|right|350px|Fig. 1. ''T'' > ''T''<sub>0</sub>. (I): Carnot engine E moves heat from heat reservoir R to | {{Image|Entropy.png|right|350px|Fig. 1. ''T'' > ''T''<sub>0</sub>. (I): Carnot engine ''E'' moves heat from heat reservoir ''R'' to closed system ''C'' and needs input of work DW<sub>in</sub>. (II): E generates work DW<sub>out</sub> from the heat flow from C to R. }}. | ||
In figure 1 a finite heat bath C ("condensor")<ref>Because of a certain similarity of C with the condensor of a steam engine C is referred as "condensor". The quotes are used to remind us that nothing condenses, unlike the steam engine where steam condenses to water</ref> of constant volume and variable temperature ''T'' is shown. It is connected to an infinite heat reservoir R through a reversible Carnot engine E. Because R is infinite its temperature ''T''<sub>0</sub> is constant, addition or extraction of heat does not change ''T''<sub>0</sub>. It is assumed that always ''T'' ≥ ''T''<sub>0</sub>. One may think of the system E-plus-C as a ship and the heat reservoir R as the sea. The following argument then deals with an attempt of extracting energy from the sea in order to move the ship, i.e., with an attempt to let E perform net outgoing work in a cyclic (i.e., along a closed path in the state space of C) process. | In figure 1 a finite heat bath C ("condensor")<ref>Because of a certain similarity of C with the condensor of a steam engine C is referred as "condensor". The quotes are used to remind us that nothing condenses, unlike the steam engine where steam condenses to water</ref> of constant volume and variable temperature ''T'' is shown. It is connected to an infinite heat reservoir R through a reversible Carnot engine E. Because R is infinite its temperature ''T''<sub>0</sub> is constant, addition or extraction of heat does not change ''T''<sub>0</sub>. It is assumed that always ''T'' ≥ ''T''<sub>0</sub>. One may think of the system E-plus-C as a ship and the heat reservoir R as the sea. The following argument then deals with an attempt of extracting energy from the sea in order to move the ship, i.e., with an attempt to let E perform net outgoing work in a cyclic (i.e., along a closed path in the state space of C) process. | ||
Revision as of 07:35, 5 November 2009
Entropy is a function of the state of a thermodynamic system. It is a size-extensive[1] quantity with dimension energy divided by temperature (SI unit: joule/K). Entropy has no clear analogous mechanical meaning—unlike volume, a similar size-extensive state parameter with dimension energy divided by pressure. Moreover entropy cannot directly be measured, there is no such thing as an entropy meter, whereas state parameters as volume and temperature are easily determined. Consequently entropy is one of the least understood concepts in physics.[2]
The state variable "entropy" was introduced by Rudolf Clausius in the 1860s[3] when he gave a mathematical formulation of the second law of thermodynamics. He derived the name from the classical Greek ἐν + τροπή (en = in, at; tropè = change, transformation). On purpose Clausius chose a term similar to "energy", because of the close relationship between the two concepts.
The traditional way of introducing entropy is by means of a Carnot engine, an abstract engine conceived in 1824 by Sadi Carnot[4] as an idealization of a steam engine. Carnot's work foreshadowed the second law of thermodynamics. The "engineering" manner of introducing entropy through an engine will be discussed below. In this approach, entropy is the amount of heat (per degree kelvin) gained or lost by a thermodynamic system that makes a transition from one state to another.
In 1877 Ludwig Boltzmann[5] gave a definition of entropy in the context of the kinetic gas theory, a branch of physics that developed into statistical thermodynamics. Boltzmann's definition of entropy was furthered by John von Neumann[6] to a quantum statistical definition. The quantum statistical point of view, too, will be reviewed in the present article. In the statistical approach the entropy of an isolated (constant energy) system is kB lnΩ, where kB is Boltzmann's constant, Ω is the number of different wave functions of the system belonging to the system's energy (Ω is the degree of degeneracy, the probability that a state is described by one of the Ω wave functions), and the function ln stands for the natural (base e) logarithm.
Not satisfied with the engineering type of argument, the mathematician Constantin Carathéodory gave in 1909 a new axiomatic formulation of entropy and the second law.[7] His theory was based on Pfaffian differential equations. His axiom replaced the earlier Kelvin-Planck and the equivalent Clausius formulation of the second law and did not need Carnot engines. Caratheodory's work was taken up by Max Born,[8] and it is treated in a few textbooks.[9] Since it requires more mathematical knowledge than the traditional approach based on Carnot engines, and since this mathematical knowledge is not needed by most students of thermodynamics, the traditional approach is still dominant in the majority of introductory works on thermodynamics.
Classical definition
The state (a point in state space) of a thermodynamic system is characterized by a number of variables, such as pressure p, temperature T, amount of substance n, volume V, etc. Any thermodynamic parameter can be seen as a function of an arbitrary independent set of other thermodynamic variables, hence the terms "property", "parameter", "variable" and "function" are used interchangeably. The number of independent thermodynamic variables of a system is equal to the number of energy contacts of the system with its surroundings.
An example of a reversible (quasi-static) energy contact is offered by the prototype thermodynamical system, a gas-filled cylinder with piston. Such a cylinder can perform work on its surroundings,
where dV stands for a small increment of the volume V of the cylinder, p is the pressure inside the cylinder and DW stands for a small amount of work. Work by expansion is a form of energy contact between the cylinder and its surroundings. This process can be reverted, the volume of the cylinder can be decreased, the gas is compressed and the surroundings perform work DW = pdV < 0 on the cylinder.
The small amount of work is indicated by D, and not by d, because DW is not necessarily a differential of a function. However, when we divide DW by p the quantity DW/p becomes obviously equal to the differential dV of the differentiable state function V. State functions depend only on the actual values of the thermodynamic parameters (they are local in state space), and not on the path along which the state was reached (the history of the state). Mathematically this means that integration from point 1 to point 2 along path I in state space is equal to integration along a different path II,
The amount of work (divided by p) performed reversibly along path I is equal to the amount of work (divided by p) along path II. This condition is necessary and sufficient that DW/p is the differential of a state function. So, although DW is not a differential, the quotient DW/p is one.
Reversible absorption of a small amount of heat DQ is another energy contact of a system with its surroundings; DQ is again not a differential of a certain function. In a completely analogous manner to DW/p, the following result can be shown for the heat DQ (divided by T) absorbed reversibly by the system along two different paths (along both paths the absorption is reversible):
(1)
Hence the quantity dS defined by
is the differential of a state variable S, the entropy of the system. In the next subsection equation (1) will be proved from the Clausius/Kelvin principle. Observe that this definition of entropy only fixes entropy differences:
Note further that entropy has the dimension energy per degree temperature (joule per degree kelvin) and recalling the first law of thermodynamics (the differential dU of the internal energy satisfies dU = DQ − DW), it follows that
(For convenience sake only a single work term was considered here, namely DW = pdV, work done by the system). The internal energy is an extensive quantity. The temperature T is an intensive property, independent of the size of the system. It follows that the entropy S is an extensive property. In that sense the entropy resembles the volume of the system. We reiterate that volume is a state function with a well-defined mechanical meaning, whereas entropy is introduced by analogy and is not easily visualized. Indeed, as is shown in the next subsection, it requires a fairly elaborate reasoning to prove that S is a state function, i.e., that equation (1) holds.
Proof that entropy is a state function
Equation (1) gives the sufficient condition that the entropy S is a state function. The standard proof, as given now, is physical, by means of Carnot cycles, and is based on the Clausius/Kelvin formulation of the second law given in the introduction.
.
In figure 1 a finite heat bath C ("condensor")[10] of constant volume and variable temperature T is shown. It is connected to an infinite heat reservoir R through a reversible Carnot engine E. Because R is infinite its temperature T0 is constant, addition or extraction of heat does not change T0. It is assumed that always T ≥ T0. One may think of the system E-plus-C as a ship and the heat reservoir R as the sea. The following argument then deals with an attempt of extracting energy from the sea in order to move the ship, i.e., with an attempt to let E perform net outgoing work in a cyclic (i.e., along a closed path in the state space of C) process.
A Carnot engine performs reversible cycles (in the state space of E, not be confused with cycles in the state space of C) and per cycle either generates work DWout when heat is transported from high temperature to low temperature (II), or needs work DWin when heat is transported from low to high temperature (I), in accordance with the Clausius/Kelvin formulation of the second law.
The definition of thermodynamical temperature (a positive quantity) is such that for II,
while for I
The first law of thermodynamics states for I and II, respectively,
For I,
For II we find the same result,
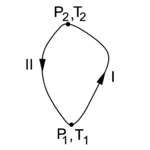
In figure 2 the state diagram of the "condensor" C is shown. Along path I the Carnot engine needs input of work to transport heat from the colder reservoir R to the hotter C and the absorption of heat by C raises its temperature and pressure. Integration of DWin = DQ − DQ0 (that is, summation over many cycles of the engine E) along path I gives
Along path II the Carnot engine delivers work while transporting heat from C to R. Integration of DWout = DQ − DQ0 along path II gives
Assume now that the amount of heat Qout extracted (along path II) from C and the heat Qin delivered (along I) to C are the same in absolute value. In other words, after having gone along a closed path in the state diagram of figure 2, the condensor C has not gained or lost heat. That is,
then
If the total net work Win + Wout is positive (outgoing), this work is done by heat obtained from R, which is not possible because of the Clausius/Kelvin principle. If the total net work Win + Wout is negative, then by inverting all reversible processes, i.e., by going down path I and going up along II, the net work changes sign and becomes positive (outgoing). Again the Clausius/Kelvin principle is violated. The conclusion is that the net work is zero and that
From this independence of path it is concluded that
is a state (local) variable.
Footnotes
- ↑ A size-extensive property of a system becomes x times larger when the system is enlarged by a factor x, provided all intensive parameters remain the same upon the enlargement. Intensive parameters, like temperature, density, and pressure, are independent of size.
- ↑ It is reported that in a conversation with Claude Shannon, John (Johann) von Neumann said: "In the second place, and more important, nobody knows what entropy really is [..]”. M. Tribus, E. C. McIrvine, Energy and information, Scientific American, vol. 224 (September 1971), pp. 178–184.
- ↑ R. J. E. Clausius, Abhandlungen über die mechanische Wärmetheorie [Treatise on the mechanical theory of heat], two volumes, F. Vieweg, Braunschweig, (1864-1867).
- ↑ S. Carnot, Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (Reflections on the motive power of fire and on machines suited to develop that power), Chez Bachelier, Paris (1824).
- ↑ L. Boltzmann, Über die Beziehung zwischen dem zweiten Hauptsatz der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht, [On the relation between the second fundamental law of the mechanical theory of heat and the probability calculus with respect to the theorems of heat equilibrium] Wiener Berichte vol. 76, pp. 373-435 (1877)
- ↑ J. von Neumann, Mathematische Grundlagen der Quantenmechnik, [Mathematical foundation of quantum mechanics] Springer, Berlin (1932)
- ↑ C. Carathéodory, Untersuchungen über die Grundlagen der Thermodynamik [Investigation on the foundations of thermodynamics], Mathematische Annalen, vol. 67, pp. 355-386 (1909).
- ↑ M. Born, Physikalische Zeitschrift, vol. 22, p. 218, 249, 282 (1922)
- ↑ H. B. Callen, Thermodynamics and an Introduction to Thermostatistics. John Wiley and Sons, New York, 2nd edition, (1965); E. A. Guggenheim, Thermodynamics, North-Holland, Amsterdam, 5th edition (1967)
- ↑ Because of a certain similarity of C with the condensor of a steam engine C is referred as "condensor". The quotes are used to remind us that nothing condenses, unlike the steam engine where steam condenses to water
References
- M. W. Zemansky, Kelvin and Caratheodory—A Reconciliation, American Journal of Physics Vol. 34, pp. 914-920 (1966) [1]