Newton's method
Newton's method, also called the Newton-Raphson method, is a numerical root-finding algorithm: a method for finding where a function obtains the value zero, or in other words, solving the equation . Most root-finding algorithms used in practice are variations of Newton's method.
Description of the algorithm
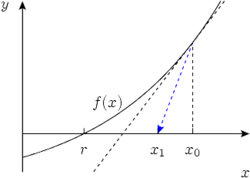
Suppose the function has a root at . The idea behind Newton's method is that, if is a smooth function, its graph can be approximated around a point by its tangent at . If the approximation is good enough, the point where the tangent crosses the -axis must lie close to . This suggests that if we choose the point to lie somewhere close to , the point where the tangent crosses the -axis — we may call that point — will lie even closer to . The idea is illustrated in the following diagram:
Now suppose that really does lie closer to than . Then we can determine the tangent of at to obtain a second point that lies closer still. More generally, given , we can obtain a better approximation .
Newton's method hinges on the fact that we can calculate the root of a tangent line directly from its straight-line equation , and that we can calculate and in terms of the function value and the function's derivative at the same point, . Put together, the relation between and can be expressed as
This formula defines Newton's method. Using it to obtain an improved approximation is called to perform a Newton step, Newton update or Newton iteration. Newton's method consists of repeatedly using this formula to obtain a sequence of successively better estimates for .
Let us illustrate Newton's method with a concrete numerical example. The golden ratio (φ ≈ 1.618) is the largest root of the polynomial ; to calculate this root, we can use the Newton iteration
with the initial estimate . Using double-precision floating-point arithmetic, which amounts to a precision of roughly 16 decimal digits, Newton's method produces the following sequence of approximations:
- x0 = 1.0
- x1 = 2.0
- x2 = 1.6666666666666667
- x3 = 1.6190476190476191
- x4 = 1.6180344478216817
- x5 = 1.618033988749989
- x6 = 1.6180339887498947
- x7 = 1.6180339887498949
- x8 = 1.6180339887498949
Since the last iteration does not change the value, we can be reasonably sure to have obtained a value for the golden ratio that is correct to the precision used. It can be seen that each iteration roughly doubles the number of correct digits. We say that the rate of convergence is quadratic. Newton's method typically — but not always — achieves such fast convergence.
Convergence analysis
Intuitively, Newton's method is based on the idea that a continuous function f can be approximated locally by a line. If both the root r and the initial guess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} lie in a region where f is sufficiently well-behaved — we may call such an area a region of convergence, Newton's method is guaranteed to converge to the root.
The convergence rate of Newton's method can be derived using Taylor series. Taking the Taylor series of f around xk gives
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(r) = 0 = f(x_k) + f'(x_k)(r-x_k) + \frac{1}{2} f''(\xi_k)(r-x_k)^2}
where . Assuming Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x_k) \neq 0} , dividing through gives
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 = \frac{f(x_k)}{f'(x_k)} - x_k + r + \frac{1}{2} \frac{f''(\xi_k)}{f'(x_k)}(r-x_k)^2.}
Moving terms to the left hand side and substituting the Newton update expression for xk+1 then gives
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1} - r = \frac{1}{2} \frac{f''(\xi_k)}{f'(x_k)}(r-x_k)^2}
and a final division shows that
This is the expression for a rate of convergence that is at least quadratic. If the second derivative Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f''} vanishes near the root, the convergence is faster than quadratic. However, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(r) = 0} , meaning that f has a double root, the result becomes slightly different: it can then be shown that the convergence is only linear.
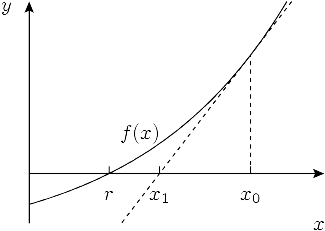
Most functions do not globally resemble lines: in general, function graphs contain curvature, stationary points, and discontinuities. Does Newton's method work in these cases? The answer is maybe. If we start with an initial guess that lies outside a region of convergence, Newton's method produces a sequence of numbers that may jump back and forth erratically or even gradually move away from the root. If we are lucky, a value eventually ends up a region of convergence. But if we are unlucky, Newton's method may entirely fail to converge.
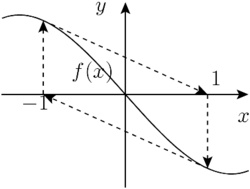
For example, if Newton's method is used to solve the equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^3 - 5x = 0} with the initial guess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0 = 1} , it will produce the endlessly repeating sequence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1, -1, 1, -1, 1, ...} .
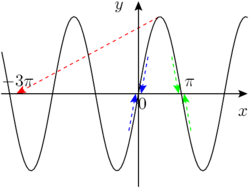
It may also happen that Newton's method converges to a root, but the wrong one. For example, if we attempt to calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} as the smallest positive solution to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin x = 0} , we must choose an initial value close to 3.14. Newton's method started near 0 would converge to 0; if started near 6.28, it would converge to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi} . If we start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} close to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi/2} , where the sine curve is horizontal, may end up close to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \pi} for some enormous n.
Complex functions
Newton's method also works for complex functions, but its convergence behavior become more intricate.
Leads to Newton fractals.
Newton's method as an optimization algorithm
Instead iterate
Multidimensional version
Gauss-Newton's method
Variations and practical implementation concerns
Damped, bracketed and hybrid methods
The fact that Newton's method may converge slowly or fail to converge for functions with horizontal tangents, or when given poor initial values, makes it unsuitable in raw form as a general-purpose root-finding algorithm. It is therefore typically combined with some mechanism for detecting and correcting convergence failure.
One way to detect failure is count the number of iterations and break if the number exceeds some specified limit. Another technique is bracketing: the root is supplied along with known bounds for its location. Failure is signaled if the Newton iteration produces a value that lies outside the bounds.
In case of failure, it may be possible to recover by switching to a slower but safer algorithm, such as the bisection algorithm. After taking a few steps with the safe method, one can switch back to Newton's method and try again. This is called a hybrid method. Another option is the damped Newton's method, in which the derivative is multiplied by a damping factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} , with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < \alpha < 1} .
Quasi-Newton methods
Newton's method requires that the derivative of the object function be known, but in some situations the derivative or Jacobian may be unavailable or prohibitively expensive to calculate. The cost can be higher still when Newton's method is used as an optimization algorithm, in which case the second derivative or Hessian is also needed.
An alternative in these situations is to use an approximation of the derivative or second-derivative, which leads to so-called quasi-Newton methods. The most common strategy is to use the function values from two successive iterations to calculate a finite difference approximation for the derivative. This is equivalent to the secant method and reduces the rate of convergence from 2 to 1.618 (more precisely, the golden ratio). An alternative is to compute a value for the derivative or second derivative accurately, but reusing the same value for several successive iterations.
Modifications of Newton's method can also lead to more specialized algorithms, such as the Durand-Kerner method which is used to find simultaneous roots of a polynomial.
Calculating inverse functions
Using Newton's method as described above, the time complexity of finding a simple root of a function f with n-digit precision is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O((\log n) F(n))} where F is the cost of calculating Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f/f'} with n-digit precision. If f can be evaluated with variable precision, the algorithm can be improved. Because of the "self-correcting" nature of Newton's method, it is only necessary to use m-digit precision at a step where the approximation has m-digit accuracy. Hence, the first iteration can be performed with a precision twice as high as the accuracy of x0, the second iteration with a precision four times as high, and so on. If the precision levels are chosen suitably, only the final iteration requires f and its derivative to be evaluated at full n-digit precision. Provided that F grows superlinearly, which is the case in practice, the cost of finding a root is thus only Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O(F(n))} .
Root-finding is essentially the same thing as calculating an inverse function. Hence, due to the aforementioned result, two differentiable functions that are inverse functions of each other have equivalent computational complexity and can be calculated in terms of each other in practice using Newton's method. In particular, it can be shown that:
- The exponential function, the natural logarithm, the trigonometric functions, and the inverse trigonometric functions, are all equivalent
- The algebraic operations of multiplication, division, and square root extraction are equivalent
During the second half of the 20th century, very efficient algorithms were found for multiplying large numbers and calculating high-precision natural logarithms with the aid of computers. Combined with Newton's method, all of the functions listed above can be calculated with this efficiency.
History
Newton's method was described by Isaac Newton in De analysi per aequationes numero terminorum infinitas (written in 1669, published in 1711 by William Jones) and in De metodis fluxionum et serierum infinitarum (written in 1671, translated and published as Method of Fluxions in 1736 by John Colson). However, his description differs substantially from the modern description given above: Newton applies the method only to polynomials. He does not compute the successive approximations xk, but computes a sequence of polynomials and only at the end, he arrives at an approximation for the root r. Finally, Newton views the method as purely algebraic and fails to notice the connection with calculus. Isaac Newton probably derived his method from a similar but less precise method by François Viète. The essence of Viète's method can be found in the work of Sharaf al-Din al-Tusi.
Newton's method was first published in 1685 in A Treatise of Algebra both Historical and Practical by John Wallis. In 1690, Joseph Raphson published a simplified description in Analysis aequationum universalis. Raphson again viewed Newton's method purely as an algebraic method and restricted its use to polynomials, but he describes the method in terms of the successive approximations xk instead of the more complicated sequence of polynomials used by Newton. Finally, in 1740, Thomas Simpson described Newton's method as an iterative methods for solving general nonlinear equations using fluxional calculus, essentially giving the description above. In the same publication, Simpson also gives the generalization to systems of two equations and notes that Newton's method can be used for solving optimization problems by setting the gradient to zero.
References
- Michael T. Heath (2002), Scientific Computing: An Introductory Survey, Second Edition, McGraw-Hill
- Jonathan M. Borwein & Peter B. Borwein (1987), Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Wiley Interscience
- Tjalling J. Ypma (1995), Historical development of the Newton-Raphson method, SIAM Review 37 (4), 531–551.


























![{\displaystyle \xi _{k}\in [r,x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5b4541fd20e7a356be47b342c4adf48e89b4100)