User:John R. Brews/Coriolis force

The Coriolis force is a force experienced by a object traversing a path in a rotating framework that is proportional to its speed and also to the sine of the angle between its direction of movement and the axis of rotation. It is one of three such inertial forces that appear in an accelerating frame of reference due to the acceleration of the frame, the other two being the centrifugal force and the Euler force. The mathematical expression for the Coriolis force appeared in an 1835 paper by a French scientist Gaspard-Gustave Coriolis in connection with the theory of water wheels, and also in the tidal equations of Pierre-Simon Laplace in 1778.

Although sometimes referred to as an apparent force, it can have very real effects.

Reference frames

Newton's laws of motion are expressed for observations made in an inertial frame of reference, that is, in any frame of reference that is in straight-line motion at constant speed relative to the "fixed stars", an historical reference taken today to refer to the entire universe. However, everyday experience does not take place in such a reference frame. For example, we live upon planet Earth, which rotates about its axis (an accelerated motion), orbits the Sun (another accelerated motion), and moves with the Milky Way (still another accelerated motion).

The question then arises as to how to connect experiences in accelerating frames with Newton's laws that are not formulated for such situations. The answer lies in the introduction of inertial forces, which are forces observed in the accelerating reference frame, due to its motion, but are not forces recognized in an inertial frame. These inertial forces are included in Newton's laws of motion, and with their inclusion Newton's laws work just as they would in an inertial frame. Coriolis force is one of these inertial forces, the other two being the centrifugal force and the Euler force.

These motions are slight, but the Coriolis force does affect aiming artillery pieces and plotting transoceanic air flights. The way Coriolis forces work is illustrated below by a few examples.

Carousel

(PD) Image: John R. Brews
Tossed ball on carousel. At the center of the carousel, the path is a straight line for a stationary observer, and is an arc for a rotating observer.

(PD) Image: John R. Brews
From the center of curvature of the path, the ball executes uniform circular motion.

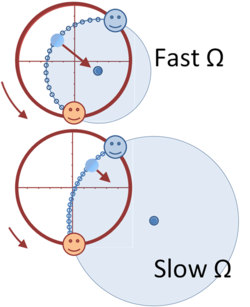
The rotating carousel is perhaps the most common example used to illustrate the effects of rotation upon the formulation of Newton's laws of motion and the introduction of inertial forces into these laws. A simple case is playing catch on the carousel. Standing on the rim of the carousel, a ball is tossed to another player standing at a different position on the rim.

As shown in the figure, from the viewpoint of a stationary observer, the tossed ball is a free body (apart from downward gravity) so its horizontal motion is that of a free body: a straight line at constant speed. The catcher of the ball rotates during the flight of the ball, so the tosser must anticipate just where the catcher will be and tosses the ball toward that future position, rather than directly at the catcher.

From the viewpoint of an observer at the center of the carousel but rotating with it, both the person tossing the ball and the catcher are standing at fixed locations, as they both turn with the carousel. However, the tosser cannot toss the ball directly toward the catcher, because the ball veers off to the right, assuming the carousel in counter-clockwise rotation. To the rotating observer, the curved path means that Newton's laws require a force to cause the ball to curve. The intuitive reaction is that the ball is pushed to the right during flight, and so this force must be countered by throwing the ball somewhat to the left.

From the spacing of the points marked on the figure it may be seen that the ball moves more rapidly for the rotating observer. That can be understood as an increased speed because the carousel is rotating, moving toward the ball. To put it differently, the curved path is longer than the straight one seen by the inertial observer, so the ball has to move faster to cover the curved path in the same time.

For both the rotating and the fixed observer, the distance of the ball from the center of the carousel at any moment in time is exactly the same, as shown by the arrows in the figure that indicate the moment of closest approach of the ball to the center.

The lower figure illustrates that to the rotating observer the ball executes a uniform circular motion about its center of curvature. The center of curvature of the path is displaced from the center of the carousel by a greater amount the slower the rate of rotation. According to the rotating observer, the ball is subject to a centripetal force directed toward the center of curvature, as shown by the arrow. As the rate of rotation slows to zero, the centripetal force drops to zero as the center of curvature recedes to infinity, and the path is the straight-line toss to the catcher.

Inertial frame

(PD) Image: John R. Brews
Some useful notation for the ball toss on a carousel.

In the stationary frame, the path of the ball is given in x,y coordinates as:

${\begin{aligned}x&=vt\ \cos \theta \\y&=-R+vt\ \sin \theta \ ,\\\end{aligned}}$

where R is the radius of the carousel, θ is the angle of launch of the ball, v is the speed of launch, and t is the time. At t=0, the tosser is at 6 o'clock, as viewed in the figure, and θ is the angle from the horizontal to the line of throw. The catcher at this time is an angle φ from 3 o'clock. If the carousel turns at the rate Ω, then the catcher has turned from the starting position by an angle Ωt_c, placing the catcher in position provided:

$2\theta =\Omega t_{c}+\varphi +\pi /2\ ,$

where t_c is the time of the catch and φ is the starting angle of the catcher. This equation results from the lower diagram and the equality of corresponding angles of parallel lines:

$\theta =(\varphi +\Omega t_{c})+(\pi /2-\theta )\ .$

The ball arrives at the rim for the arriving catcher when the path length equals the chord of the circle:

$vt_{c}=2R\ \sin \theta \ .$

These two equations either determine the angle of launch in terms of a known speed by use of a nonlinear equation or, by assuming a time of catch, the first equation determines the angle of launch and the last equation determines the necessary speed of throw:

$v=2{\frac {R}{t_{c}}}\ \sin \left({\frac {\Omega t_{c}+\varphi +\pi /2}{2}}\right)\ .$

Rotating frame

(PD) Image: John R. Brews
The inertial forces on the ball combine to provide the resultant centrifugal force required by Newton's laws for circular motion.

The description in the rotating frame is more complex than in the inertial frame. One approach to the analysis of this case is to observe that for the rotating observer at the center of the carousel, the ball traces a circular path from the tosser to the catcher. The path has a radius, say ρ, measured from the center of curvature of the path, which is off-center from the carousel. To travel this circular path of radius ρ at speed v path requires a centripetal acceleration v²/ρ, where the speed v is set by the way the ball is tossed in combination with the rotation. The centripetal force mv²/ρ is determined as the inward combination of the outward centrifugal force mv²/ρ and the inward Coriolis force 2mv²/ρ as seen from the center of curvature.

The rotating observer always sees a centrifugal force related to the rotation of the carousel. Any object at distance r from the center of rotation is subject to the outward "centrifugal acceleration" Ω²r radial to the center of rotation. This acceleration is not the true centrifugal acceleration of the ball, Ω²ρ, because it is not directed radial to the center of curvature. In addition to this inertial force, if an object is seen by the rotating observer to move with a vector velocity v, it is subject to a Coriolis acceleration a_Cor = 2v × Ω, which is in the plane of the carousel and perpendicular to the velocity, as shown in the figure. These two inertial forces combine to form a resultant centripetal acceleration a_ctpl with magnitude a_ctpl = Ω²ρ pointing inward to the center of curvature, as required by Newton's laws for circular motion.

Here is a question: given the radius of the turntable R, the rate of angular rotation Ω, and the speed of the ball (assumed constant) v, what is the correct angle θ to aim so as to hit the target at the edge of the turntable?

The inertial frame of reference provides one way to handle the question: calculate the time to interception, which is t_f = R / v . Then, the turntable revolves an angle Ω t_f in this time. If the ball toss is directed at an angle θ = Ω t_f = Ω R / v, then the ball arrives at the periphery at the same time as the target.

No discussion of Coriolis force can arrive at this solution as simply, so the reason to treat this problem is to demonstrate Coriolis formalism in an easily visualized situation.

The trajectory in the inertial frame (denoted A) is a straight line radial path at angle θ. The position of the ball in (x, y) coordinates at time t is:

$\mathbf {r} _{A}(t)=vt\ \left(\cos \theta ,\right.$$\left.{\color {white}..}\ \sin \theta \right)\ .$

In the turntable frame (denoted B), the x- y axes rotate at angular rate Ω , so the trajectory becomes:

$\mathbf {r} _{B}(t)$   $=vt\ \left(\cos(\theta -\Omega t),\right.$$\left.{\color {white}..}\sin(\theta -\Omega t)\right)\ .$

To determine the components of acceleration, a general expression is used from the article inertial forces:

$\mathbf {a} _{B}=\mathbf {a} _{A}-2{\boldsymbol {\Omega }}\times \mathbf {v} _{B}-{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times \mathbf {r} _{B})-{\frac {d{\boldsymbol {\Omega }}}{dt}}\times \mathbf {r} _{B}\ ,$

in which the term in Ω × v_B is the Coriolis acceleration and the term in Ω × ( Ω × r_B) is the centrifugal acceleration. The results are (let α = θ − Ω t):

${\boldsymbol {\Omega }}\mathbf {\times r_{B}} ={\begin{vmatrix}{\boldsymbol {i}}&{\boldsymbol {j}}&{\boldsymbol {k}}\\0&0&\Omega \\vt\cos \alpha &vt\sin \alpha &0\end{vmatrix}}\ =\Omega tv\left(-\sin \alpha ,\cos \alpha \right)\ ,$

${\boldsymbol {\Omega \ \times }}\left({\boldsymbol {\Omega }}\mathbf {\times r_{B}} \right)={\begin{vmatrix}{\boldsymbol {i}}&{\boldsymbol {j}}&{\boldsymbol {k}}\\0&0&\Omega \\-\Omega tv\sin \alpha &\Omega tv\cos \alpha &0\end{vmatrix}}\ \ ,$

producing a centrifugal acceleration:

$\mathbf {a_{\mathrm {Cfgl} }} =\Omega ^{2}vt\left(\cos \alpha ,\sin \alpha \right)=\Omega ^{2}\mathbf {r_{B}} (t)\ .$

Also:

$\mathbf {v_{B}} ={\frac {d\mathbf {r_{B}} (t)}{dt}}=(v\cos \alpha +\Omega t\ v\sin \alpha ,\ v\sin \alpha -\Omega t\ v\cos \alpha ,\ 0)\ \ ,$

${\boldsymbol {\Omega }}\mathbf {\times v_{B}} ={\begin{vmatrix}\!{\boldsymbol {i}}&\!{\boldsymbol {j}}&\!{\boldsymbol {k}}\\0&0&\Omega \\v\cos \alpha \quad &v\sin \alpha \quad &\quad \\\;+\Omega t\ v\sin \alpha &\;-\Omega t\ v\cos \alpha &0\end{vmatrix}}\ \ ,$

producing a Coriolis acceleration:

$\mathbf {a_{\mathrm {Cor} }} =-2\left[-\Omega v\left(\sin \alpha -\Omega t\cos \alpha \right),\right.$$\left.{\color {white}...}\ \Omega v\left(\cos \alpha +\Omega t\sin \alpha \right)\right]\$

$=2\Omega v\left(\sin \alpha ,\ -\cos \alpha \right)-2\Omega ^{2}\mathbf {r_{B}} (t)\ .$

It is seen that the Coriolis acceleration not only cancels the centrifugal acceleration, but together they provide a net "centripetal", radially inward component of acceleration (that is, directed toward the center of rotation):

$\mathbf {a_{\mathrm {Cptl} }} =-\Omega ^{2}\mathbf {r_{B}} (t)\ ,$

and an additional component of acceleration perpendicular to r_B (t):

$\mathbf {a_{C\perp }} =2\Omega v\left(\sin \alpha ,\ -\cos \alpha \right)\ .$

The "centripetal" component of acceleration resembles that for circular motion at radius r_B, while the perpendicular component is velocity dependent, increasing with the radial velocity v and directed to the right of the velocity. The situation could be described as a circular motion combined with an "apparent Coriolis acceleration" of 2Ω v. However, this is a rough labeling: a careful designation of the true centripetal force refers to a local reference frame that employs the directions normal and tangential to the path, not coordinates referred to the axis of rotation.

These results also can be obtained directly by two time differentiations of r_B (t). Agreement of the two approaches demonstrates that one could start from the general expression for fictitious acceleration above and derive the trajectories. However, working from the acceleration to the trajectory is more complicated than the reverse procedure used here, which, of course, is made possible in this example by knowing the answer in advance.

As a result of this analysis an important point appears: all the fictitious accelerations must be included to obtain the correct trajectory. In particular, besides the Coriolis acceleration, the centrifugal force plays an essential role. It is easy to get the impression from verbal discussions of the ball problem, which are focused on displaying the Coriolis effect particularly, that the Coriolis force is the only factor that must be considered; emphatically, that is not so. A turntable for which the Coriolis force is the only factor is the parabolic turntable. A somewhat more complex situation is the idealized example of flight routes over long distances, where the centrifugal force of the path and aeronautical lift are countered by gravitational attraction.

Apparent motion of stationary objects

(PD) Image: John R. Brews
Vector cross product used to determine the Coriolis force.

Though centrifugal force adequately describes the force on objects at rest relative to a steadily rotating frame of reference, the fictitious force on objects moving in the rotating frame includes the Coriolis force. In the figure, the vector Ω represents the rotation of the frame at angular rate ω; the vector v shows the velocity tangential to the circular motion as seen in the rotating frame. The vector Ω × v is found using the right-hand rule for vector cross products. It is related to the negative of the Coriolis force (the Coriolis force is −2 m Ω × v).

To deal with motion directly in a rotating frame of reference by applying Newton's laws, it is necessary to take these pseudo-forces into account. For example, consider the apparent revolution of a stationary object (such as a distant star or planet), which is in motion as viewed from the rotating frame:

A body that is stationary relative to a non-rotating inertial frame appears to be rotating when viewed from a frame rotating at angular rate Ω. Therefore, application of Newton's laws to what looks like circular motion in the rotating frame at a radius r, requires an inward centripetal force of −m Ω² r to account for the apparent circular motion. This centripetal force in the rotating frame is provided as a net fictitious force that is the sum of the radially outward centrifugal force m Ω² r and the Coriolis force −2m Ω × v_rot. To evaluate the Coriolis force, we need the velocity as seen in the rotating frame, v_rot. As explained in the Derivation section, this velocity is given by −Ω × r. This rotational motion, following the fixed stars, diminishes the apparent centrifugal force (the Eötvös effect), because the Coriolis force points inward when $2m{\boldsymbol {\Omega }}\times \left[d\mathbf {r} /dt\right]$ is evaluated for $\left[d\mathbf {r} /dt\right]$ in the direction of v_rot. This inward force has the value −2m Ω² r. The combination of the centrifugal and Coriolis force is then m Ω² r − 2m Ω² r = −m Ω² r, exactly the centripetal force required by Newton's laws for circular motion.

Derivation

See also: Inertial force

Velocity

In a rotating frame of reference bodies can have the same positions as in a nonrotating frame, but they will move differently due to the rotation of the frame. Consequently, the time derivatives of any position vector r depending on time (velocity dr/dt and acceleration d²r/dt²) will differ according to the rotation. When time derivative [dr/dt] is evaluated from a reference frame with a coincident origin at r=0 but rotating with the absolute angular velocity Ω:

${\frac {\operatorname {d} {\boldsymbol {r}}}{\operatorname {d} t}}=\left[{\frac {\operatorname {d} {\boldsymbol {r}}}{\operatorname {d} t}}\right]+{\boldsymbol {\Omega }}\times {\boldsymbol {r}}\ ,$

where × denotes the vector cross product and square brackets '[…]' denote evaluation in the rotating frame of reference. In other words, the apparent velocity in the rotating frame is altered by the amount of the apparent rotation ${\boldsymbol {\Omega }}\times {\boldsymbol {r}}$ at each point, which is perpendicular to both the vector from the origin 'r' and the axis of rotation 'Ω' and directly proportional in magnitude to each of them. The vector 'Ω' has magnitude 'Ω' equal to the rate of rotation and is directed along the axis of rotation according to the right-hand rule. The angle must be measured in radians per unit of time.

Acceleration

Newton's law of motion for a particle of mass m can be written in vector form as

${\boldsymbol {F}}=m{\boldsymbol {a}}\ ,$

where 'F' is the vector sum of the physical forces applied to the particle and 'a' is the absolute acceleration of the particle, given by:

${\boldsymbol {a}}={\frac {\operatorname {d} ^{2}{\boldsymbol {r}}}{\operatorname {d} t^{2}}}\ ,$

where 'r' is the position vector of the particle. The differentiations are performed in the inertial frame.

By twice applying the transformation above from the inertial to the rotating frame, the absolute acceleration of the particle can be written as:

${\begin{aligned}{\boldsymbol {a}}&={\frac {\operatorname {d} ^{2}{\boldsymbol {r}}}{\operatorname {d} t^{2}}}={\frac {\operatorname {d} }{\operatorname {d} t}}{\frac {\operatorname {d} {\boldsymbol {r}}}{\operatorname {d} t}}={\frac {\operatorname {d} }{\operatorname {d} t}}\left(\left[{\frac {\operatorname {d} {\boldsymbol {r}}}{\operatorname {d} t}}\right]+{\boldsymbol {\Omega }}\times {\boldsymbol {r}}\ \right)\\&=\left[{\frac {\operatorname {d} ^{2}{\boldsymbol {r}}}{\operatorname {d} t^{2}}}\right]+{\frac {\operatorname {d} {\boldsymbol {\Omega }}}{\operatorname {d} t}}\times {\boldsymbol {r}}+2{\boldsymbol {\Omega }}\times \left[{\frac {\operatorname {d} {\boldsymbol {r}}}{\operatorname {d} t}}\right]+{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})\ .\end{aligned}}$

Force

The apparent acceleration in the rotating frame is [d²r/dt²]. An observer unaware of the rotation would expect this to be zero in the absence of outside forces. However Newton's first law applies only in the inertial frame, to the absolute acceleration d²r/dt². Therefore the observer perceives the extra terms as accelerations imposed by fictitious forces. These terms in the apparent acceleration are independent of mass; so it appears that each of these fictitious forces, like gravity, pulls on an object in proportion to its mass. When these forces are added, the equation of motion has the form:

${\boldsymbol {F}}-m{\frac {\operatorname {d} {\boldsymbol {\Omega }}}{\operatorname {d} t}}\times {\boldsymbol {r}}-2m{\boldsymbol {\Omega }}\times \left[{\frac {\operatorname {d} \mathbf {r} }{\operatorname {d} t}}\right]-m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})$ $=m\left[{\frac {\operatorname {d} ^{2}{\boldsymbol {r}}}{\operatorname {d} t^{2}}}\right]\ ,$

which, from a formal mathematical standpoint, is the same result as simply moving the extra acceleration terms to the left hand side (the force side) of the equation. From the viewpoint of the rotating frame, however, the terms on the force side all result from forces really experienced as forces. The terms on the force side of the equation can be recognized as the Euler force $m\operatorname {d} {\boldsymbol {\Omega }}/\operatorname {d} t\times {\boldsymbol {r}}$, the Coriolis force $2m{\boldsymbol {\Omega }}\times \left[\operatorname {d} {\boldsymbol {r}}/\operatorname {d} t\right]$, and the centrifugal force $m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})$, respectively. The centrifugal force points directly away from the axis of rotation of the rotating reference frame, with magnitude mΩ²r.

Notice that for a non-rotating inertial frame of reference $({\boldsymbol {\Omega }}=0)$ the centrifugal force and all other fictitious forces disappear.

Examples

Below several examples illustrate both the inertial and rotating frames of reference, and the role of centrifugal force and its relation to Coriolis force in rotating frameworks. For more examples see Fictitious force, rotating bucket and rotating spheres.

Straight-line motions

The principles described above are illustrated by considering two example motions: (i) a straight-line motion as seen in a stationary frame, and (ii) a straight-line motion as seen in a rotating frame.

In the first case, straight line motion as seen in a stationary frame, no external force is required according to Newton's law of inertia. However, in the rotating frame, this straight-line motion appears curved; if the laws of Newtonian mechanics were to apply in this rotating frame, an external force would be required in order to account for the curved motion. These points of view can be reconciled by introducing pseudo-forces, or fictitious forces, in the rotating frame. A centrifugal force is attributed to every mass in the rotating frame. A non-zero Coriolis force also acts upon the mass if its trajectory is at an angle to the axis of rotation. In order for the rotating observer to agree with the stationary observer that no net external force acts on the mass, the sum of the centrifugal force and Coriolis force must be exactly equal to the force required by the curved motion. In this way the laws of Newtonian mechanics are now applicable in both the stationary and rotating frames of reference.

In the second case, straight-line motion as seen in a rotating frame, the roles of the observers are reversed. This time the rotating observer sees straight-line motion, and so finds no net force is required to support the motion. On the other hand, the stationary observer sees a curved motion, and so believes a external force is required. Again, these viewpoints are reconciled via fictitious forces acting on all masses in the rotating frame. If these forces are unopposed, they cause curved motion. Hence, straight-line motion observed in the rotating frame must find an external influence at work that exactly balances these fictitious forces. Thus, the two observers are in agreement once again, but in this case an external force is required for the observed motion.

Notes

http://books.google.com/books?id=-3H5V0LGBOgC&pg=PA122&dq=Foucault+pendulum&hl=en&ei=CV1gTenZOpGisQO9ruzNCA&sa=X&oi=book_result&ct=result&resnum=9&ved=0CGQQ6AEwCA#v=onepage&q=Foucault%20pendulum&f=false

http://books.google.com/books?id=NAo7yv7Jmq0C&pg=PA22&dq=Foucault+pendulum&hl=en&ei=VopgTdmBCoK4sQP6p-ncCA&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCoQ6AEwADgK#v=onepage&q=Foucault%20pendulum&f=false

http://books.google.com/books?id=NAo7yv7Jmq0C&pg=PA22&dq=Foucault+pendulum&hl=en&ei=VYVgTcujHoOusAO0vOXNCA&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCoQ6AEwADgK#v=onepage&q=Foucault%20pendulum&f=false

http://books.google.com/books?id=hrBe52GPHrYC&pg=PA351&dq=Foucault+pendulum&hl=en&ei=VYVgTcujHoOusAO0vOXNCA&sa=X&oi=book_result&ct=result&resnum=9&ved=0CFQQ6AEwCDgK#v=onepage&q=Foucault%20pendulum&f=false

http://books.google.com/books?id=GfCil84YTm4C&pg=PA116&dq=Foucault+pendulum&hl=en&ei=E4ZgTeaDGIa-sQP1zvDHCA&sa=X&oi=book_result&ct=result&resnum=8&ved=0CE0Q6AEwBzgU#v=onepage&q=Foucault%20pendulum&f=false

http://books.google.com/books?id=mms6MXH9CuoC&pg=PA22&dq=Foucault+pendulum&hl=en&ei=34ZgTeukEIuesQPMvPHYCA&sa=X&oi=book_result&ct=result&resnum=2&ved=0CCsQ6AEwATge#v=onepage&q=Foucault%20pendulum&f=false

http://books.google.com/books?id=imrm2aOs9_8C&pg=PA90&dq=Foucault+pendulum&hl=en&ei=34ZgTeukEIuesQPMvPHYCA&sa=X&oi=book_result&ct=result&resnum=7&ved=0CEQQ6AEwBjge#v=onepage&q=Foucault%20pendulum&f=false

Maxwell

http://books.google.com/books?id=wr2QOBqOBakC&pg=PA184&dq=Foucault+pendulum&hl=en&ei=U4hgTd-9Foa6sQP3lt3ACA&sa=X&oi=book_result&ct=result&resnum=2&ved=0CDAQ6AEwATgy#v=onepage&q=Foucault%20pendulum&f=false

Practical matters

http://books.google.com/books?id=sSPLspTUYEEC&pg=PA73&dq=Foucault+pendulum&hl=en&ei=U4hgTd-9Foa6sQP3lt3ACA&sa=X&oi=book_result&ct=result&resnum=4&ved=0CDsQ6AEwAzgy#v=onepage&q=Foucault%20pendulum&f=false

http://books.google.com/books?id=1J2hzvX2Xh8C&pg=PA272&dq=Foucault+pendulum&hl=en&ei=D4lgTdrSGIi6sQPrsunYCA&sa=X&oi=book_result&ct=result&resnum=3&ved=0CDIQ6AEwAjg8#v=onepage&q=Foucault%20pendulum&f=false